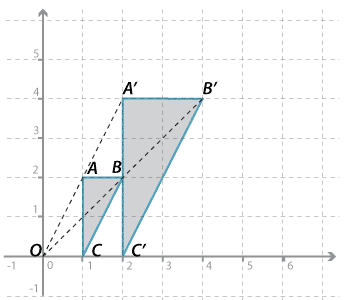Content description

Use the enlargement transformation to explain similarity and develop the conditions for triangles to be similar (ACMMG220)

Elaborations

• establishing the conditions for similarity of two triangles and comparing this to the conditions for congruence
• using the properties of similarity and ratio, and correct mathematical notation and language, to solve problems involving enlargement (for example, scale diagrams)
• using the enlargement transformation to establish similarity understanding that similarity and congruence help describe relationships between geometrical shapes and are important elements of reasoning and proof.

Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)

Enlargements

Translations, rotations and reflections are examples of congruence transformations, because the image of a figure under one of these transformations is congruent to the original. We defined two figures to be congruent if one could be mapped to the other by a sequence of these transformations.

Here a fourth type of transformation of the plane called an enlargement is introduced, in which all lengths are increased or decreased in the same ratio.

To specify an enlargement, we need to specify two things:

• the centre O of the enlargement; the centre of enlargement stays fixed in the one place, while the enlargement expands or shrinks everything else around it
• an enlargement factor k (or enlargement ratio 1 : k); the distances of all points from the enlargement centre increase or decrease by this factor.

With enlargement, lengths of sides are increased or decreased by the same enlargement factor.

Here the centre of enlargement is O and the enlargement factor is 2.

Detailed description

Note that \(OA^\prime = 2OA, OB^\prime = 2OB\) and \(OC^\prime = 2OC.\) Also, \(A^\prime B^\prime = 2AB, A^\prime C^\prime = 2AC,\) and \(B^\prime C^\prime = 2BC\).